5. 분포 (1) 분포의 정의와 정규분포, 표준정규분포

추론 통계 (Inferential statistics)

포본으로 모집단의 성질을 추정하는 것

확률 이론과 분포에 의존함

 

1️⃣ 분포(Distributions)

변량의 값이 얼마나 자주 등장할 수 있는지 보여주는 것

통계학에서 분포란 확률분포를 의미한다.

ex. 정규 분포, t-분포, 포아송분포 등

 

분포 시각화 유의 사항
분산은 값들이 어떻게 서로 연관되어 위치해 있는지를 표현할 뿐, 그래프가 아니다!

 

파라미터(parameter, 모수)

분포의 형태를 정하는 숫자

ex. 평균(\(\mu)\), 표준편차(\(\sigma)\)

 

 

2️⃣ 정규분포(Normal distribution)

가우스 분포(Gaussian distribution)이라고도 함

연속형 확률변수를 대상으로 정의

다양한 확률변수를 근사하는데 사용

표본의 크기가 클수록 정규분포에 가까워짐(중심극한정리)

 

\(N\sim(\mu, \sigma^{2})\) 으로 표현

\(N\) : 정규분포

\(\sim\) : 분포를 따른다

평균(\(\mu\))과 분산(\(\sigma^{2}\))인

 

[출처] 위키백과 - 평균과 분산을 달리한 정규분포

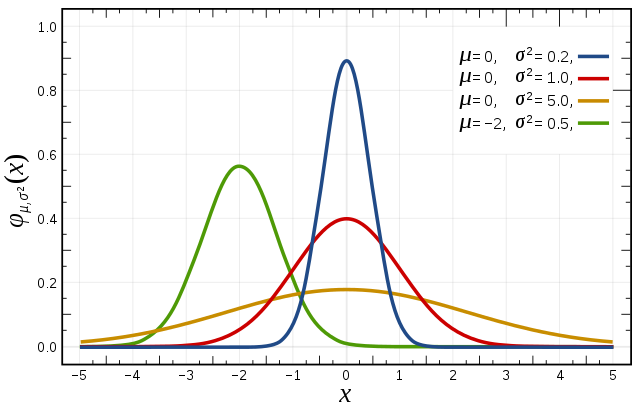
위와같이 평균(\(\mu\))은 분포의 위치를, 분산 (\(\sigma^{2}\))은 분포의 넓이를 결정하는 것을 알 수 있음

 

특징

- 평균(\(\mu\))를 중심으로 한 종(bell)모양으로 좌우대칭 분포

- mean = median = mode   => no skew

- 평균(\(\mu\)) 근처에 값이 가장 많고, 평균(\(\mu\))에서 멀어질수록 적어짐

- 정규분포로 근사할 수 있는 확률변수가 많음

 

성질

[출처] 네이버 지식백과

•  \(\mu - \sigma \sim \mu + \sigma\) 범위에 값이 있을 확률 : 약 68%

•  \(\mu - 2\sigma \sim \mu + 2\sigma\) 범위에 값이 있을 확률 : 약 95%

•  \(\mu - 3 \sigma \sim \mu + 3 \sigma\) 범위에 값이 있을 확률 : 약 99.7%

 

3️⃣ 표준정규분포(Standard normal distribution)

\(N\sim(\mu, \sigma^{2})\)인 분포

즉 평균(\(\mu\)) = 0, 분산( \(\sigma^{2}\)) = 1인 분포

 

표준화(standardizing, normalizing)

\(z = {{x - \mu}\over{\sigma}}\)

확률변수(\(x\)와 평균(\(\mu\)),  분산( \(\sigma^{2}\))을 이용하여 평균을 0, 분산을 1로 변환하는 과정

이때 위의 z값을 z-score라고 부름

 

표준화의 이점

- 다른 정규분포와 비교 가능

- 정상성(normality) 탐지 가능

- 이상치(outlier)탐지 가능

- 신뢰구간 생성 가능

- 가설 테스트 가능

- 회귀분석 수행 가능

 

 

 

 

[출처]

통계 101 X 데이터 분석, 아베 마사토, 2022

Statistics for Data Science and Business Analysis, 유데미